Three Bayesian estimates
[Update (8/17): Commenter HL sent me to a Robert Wright podcast, which is the single clearest explanation of the evidence that I’ve come across. Peter Miller is an impressive advocate for zoonosis.]
I’m on record suggesting that Covid probably entered the human population from an animal market in Wuhan. I’ve given 10-1 odds in favor of that hypothesis. Two other researchers looked at essentially the same data as I did, and reached radically different conclusions.
In a presentation at the Hoover Institute, Andrew Levin presented a paper entitled:
A Bayesian Assessment of the Origins of COVID-19 using Spatiotemporal and Zoonotic Data
Levin gave odds of 100,000,000 to 1 in favor of the lab leak hypothesis over the zoonosis hypothesis.
In a recent interview, NPR asked Michael Worobey to place odds on zoonosis vs. lab leak:
NPR: So what is the likelihood of that coincidence happening — that the first cluster of cases occurs at a market that sells animals known to be susceptible to SARS-CoV-2, but the virus didn’t actually come from the market?
I would put the odds at 1 in 10,000. But it’s interesting. We do have one analysis where we show essentially that the chance of having this pattern of cases [clustered around the market] is 1 in 10 million [if the market isn’t a source of the virus]. We consider that strong evidence in science.
Think about it. You have two people who both rational, highly respected researchers. Both look at the same data set. Both use Bayesian reasoning. One says 100,000,000-1 lab leak and one says somewhere between 10,000-1 and 10,000,000-1 zoonosis.
I’m not a highly respected researcher, but I’m looking at the same data and also using Bayesian reasoning, and I previously ended up guesstimating odds of 10-1 zoonosis.
I feel like this case is telling us something about Bayesian reasoning, but I’m not quite sure what it is. To take one example, Worobey emphasizes that most of the early cases occurred on the west side of the market, which is where the suspicious “raccoon dog” cage was located:

Levin emphasizes that none of the first 5 cases occurred immediately next to the suspicious “raccoon dog” cage, they were one aisle over:
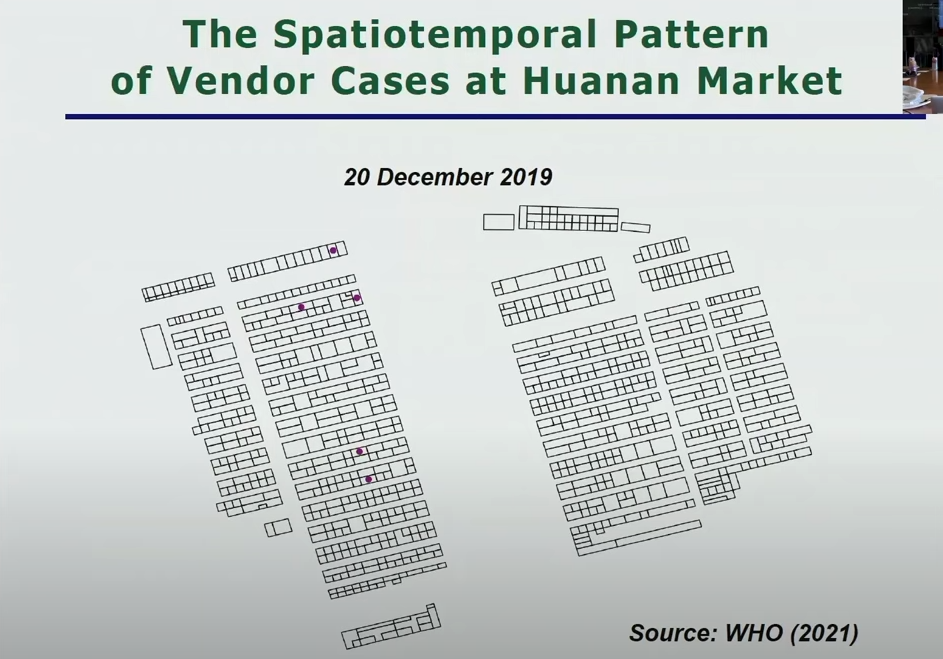
Most of the early lab leak theories focused on the famous Wuhan Institute of Virology, which is not located anywhere the animal market. Levin suggests that a lab leak could have occurred at a different lab, a CDC office near the animal market.
I have a hard time evaluating this claim. He might be correct, but the original focus on Wuhan was based on the idea that the WIV is special, not just another lab. The argument was essentially “What are the odds that the pandemic would happen in the city with this very special virology lab.” If the claim is now that the outbreak was from a different lab, doesn’t that change our priors? On the other hand, perhaps all Wuhan research labs had a special interest in these bat viruses.
One thing I like about both researchers is that they avoid a lot of unsubstantiated conspiracy theories, and focus on the spatiotemporal pattern of the outbreak. And yet even with this sort of methodological agreement, they end up about as far apart as the Earth to the Andromeda galaxy. (And I’m somewhere off in the Magellanic Clouds.)
Weird!
Tags:


16. August 2024 at 15:37
You should check out Robert Wright’s podcast with Peter Miller on the latter’s famous debate win vs. Bayesian advocates of Lab leak theory. https://youtu.be/MTxgq8fcPpU?si=FubvNRQ_nYPau–f
17. August 2024 at 04:41
The debate linked by the previous commenter was also discussed by Scott Alexander, who seems to have reached a similar probability estimate to Scott Sumner. Great minds think alike.
https://www.astralcodexten.com/p/practically-a-book-review-rootclaim
https://www.astralcodexten.com/p/highlights-from-the-comments-on-the-5d7
17. August 2024 at 05:38
A great post.
Do you believe we should ban gain of function research? If so, do you have any concern that gain of function research will continue in other countries? Are there legitimate national security concerns about a “gain of function gap” (leaving aside conspiracy theories of Brigadier General Jack Ripper)?
17. August 2024 at 08:17
Everyone, Check out the link that HL provided, it’s a very clear presentation of the evidence.
Todd, I don’t know enough about the issue to have a strong view. My biggest fear is that a future nutty eco-terrorist might use gain of function to “solve” overpopulation. Think Unibomber times one billion.
17. August 2024 at 08:50
I’ll take Scott Sumner’s word on the respected part but, based on the YouTube link above and the Hoover slides/transcript, I can show that Andrew Levin demonstrates poor reasoning and promotes demonstrably incorrect facts.
Let me start off with the good parts. First, from Slides 3 & 4: the Huanan market is a “wholesale” market consisting of 676 vendors each servicing approximately 10 (-15) customers per day. This is a nice very nice way of distinguishing this market from the archetype of a busy consumer market most of us have in our heads. Second, the 2021 WHO report had illegible maps and images that made it difficult to assess the key data. The papers by Woreby and others provided beautiful graphics of the same data. Unfortunately, the Levin’s presentation quickly went downhill from here.
See Table 1 List of 38 species sold in Wuhan City markets from the serendipitous paper Animal sales from Wuhan wet markets immediately prior to the COVID-19 pandemic. There were 38 Raccoon Dogs and 10 Palm Civets sold per month, the two intermediate hosts identified in the SARS-1 outbreak, and 10 mink (there were significant SARS-CoV-2 outbreaks in mink farms). Huanan was the largest of the four, IIRC, wildlife markets in Wuhan. The table indicates that some of the raccoon dogs and palm civets were wild caught (not just farmed) and that they were primarily sold for food. Levin shows images of raccoon dogs sold primarily for fur with the finished pelts shipped and sold northeast of Wuhan. Table 1 makes clear that live, susceptible, wild caught (i.e. illegal) mammals were being sold at Huanan. The numbers were low per species but multiple susceptible species were aggregated together at the shops and in greater numbers/density in the upstream supply chain. Levin is incredulous how the virus could spread between cages without thinking about these cages be sprayed down daily to remove feces, an ideal way to aerosolize the virus for respiratory spread or oral spread. He is also incredulous how pair bonded raccoon dogs, who lead mostly solitary lives, could be infected by wild bat viruses. For me, I look for nocturnal arboreal mammal species that live in the feeding grounds of insectivore bats that leave fresh guano in the branches they perch feed from. This only explains the first zoonotic spillover, once established in the supply chain it doesn’t need a wildlife link. I could go on.
This is false. Like SARS-1, SARS-CoV-2 can enter the cell via Clathrin-Mediated Endocytosis. The furin cleavage site allows SARS-CoV-2 to enter the cell via a second pathway: receptor-mediated fusion. The Aha! moment for me from TWiV 715: Fauci ouchy which discussed the entry mechanism in the beautifully illustrated HCQ paper linked in the shownotes. This experiment also (safely) inserted a furin cleavage site genetically in the SARS-1 spike and removed it from the SARS-CoV-2 spike to clearly show that HCQ stops endocytosis but not fusion, so it works with cells that don’t have TMPRSS2. QED. Beautiful experiment, and an example of the gift, not curse, that Doudna and Charpentier gave us with CRISPR/CAS9.
The furin cleavage site is an important characteristic of SARS-CoV-2 but I don’t think it alone accounts for its pandemic potential.
This is where I now lump Levin in with the irrational Gain-of-Function is ALWAYs EVIL activists along with Matt Ridley and other Lab-Leakers. I don’t have to wait for the paper to be published, I can safely assume that a mix of bad assumptions, already demonstrated, combined with motivated reasoning will result in a terrible Bayesian Analysis similar to what Saar Wilf generated in his debate against Peter Miller. YMMV.
17. August 2024 at 09:00
FYI: Peter Miller’s blog post The case against the lab leak theory is an excellent plain English explanation that goes well with his interview by Robert Wright.
17. August 2024 at 09:06
RAD, I am much more persuaded by Peter Miller’s presentation than Levin’s. That’s why I’m staying 10-1 zoonosis.
In one respect, Miller actually understates the argument for zoonosis. He says the first SARs began in China’s 15th largest city, and thus gives a 5% change that Wuhan would happen randomly. But Foshan is a part of metro Guangzhou, which is arguably China’s largest metro area. These things seem to happen in really big cities in south/central China. I’d up the odds to 10%.
17. August 2024 at 10:32
The thing that made Bayesian analysis so useful is that it let us incorporate prior knowledge into the work. It let us end up with probabilities that were closer to what we found in reality. However, when we are not incorporating knowledge but opinion it becomes much less useful. Miller’s analysis is so helpful because the lab leak people have made lots of claims that just arent true and he goes over those.
Steve
17. August 2024 at 20:40
Steve, Yes, his analysis is almost a perfect example of rational analysis. If someone asked me what I mean by the term ‘rational’, I’d say watch the Peter Miller video.
18. August 2024 at 02:02
Scott,
my shorthand for Bayesian reasoning is “glorified prejudice”. Because what are Bayesian priors if not literally prejudice? Now that is not a bad thing, because it incorporates prior data and knowledge, in the ideal case. But oftentimes there are no prior data or knowledge, just guesses. And this puts Bayesianism into perspective: the selective choice of priors changes everything and ultimately, between inductive reasoning and best-guessing, we have a very imperfect method, especially if one would want to come up with a numerical estimate. Grain of salt thing.
18. August 2024 at 07:02
Folks, Bayesian reasoning is a process for computing probabilities. It’s not formula that results in one answer. It’s just a process that makes ones priors and evidence transparent. We can arrive a completely different conclusions… but we can see exactly why.
Priors are similar to prejudice… as they are a measure of existing beliefs or the existing state of understanding, before accounting for new information. They are initial beliefs, they influence perception and they can be (strong priors) resistant to changing those beliefs. But they are transparent, derived from data, are flexible to updates, and so are in a sense neutral.
When someone says, well I used Bayesian reasoning to arrive at such and such… it’s a lot like saying, well I used math to estimate this. Yeah sure, now I need to see your math… lol
18. August 2024 at 07:59
mbka and Student, Good points. I have trouble understanding the concept of Bayesian reasoning, because when it’s explained to me I cannot imagine any other type of reasoning. If it’s that general, then it’s just a sort of scientific term for “rationality”.
18. August 2024 at 08:56
someone giving 100m to 1 or even 10k to 1 odds on something like Covid origin is a big red flag that their thinking is seriously flawed.
19. August 2024 at 03:17
Scott,
All probabilistic reasoning is Bayesian, whether people realize it or not. The only difference is how transparent people are with their priors.
19. August 2024 at 03:42
You do need to follow Bayes Rule though… well if you are trying to invert conditional probabilities to your beliefs about the probability of a cause. You can’t just make stuff up… My point though is that we tend to naturally think this way… but the devil is in the details.
Bayes’ Rule is a mathematical formula for inverting conditional probabilities, allowing us to update our beliefs about the probability of a cause (or hypothesis) given its effect (or observed data). It’s a way to reverse the direction of inference, moving from:
P(effect | cause) → P(cause | effect)
In other words, Bayes’ Rule helps us answer questions like:
Given that I have a positive test result (effect), what’s the probability that I have the disease (cause)?
Or
Given that it’s raining outside (effect), what’s the probability that the streets will be wet (cause)?
By inverting the conditional probabilities, Bayes’ Rule enables us to make probabilistic statements about the cause, given the observed effect.
19. August 2024 at 08:19
It’s tricky and often, meaningless trying to assign a probability ex-post and then wonder if such small probability event happened due to some “grand design”.
A person I know has just won lottery, if he’s not cheating, the chance of him winning is just one in a million, hence he must be cheating.
There are trillions of planets out there, but life somehow develops and thrives on earth, the probability is really small that this happened by chance, it must be the work of a higher being.
Bottomline, no amount of Bayesian reasoning could get you anywhere closer to the truth.
19. August 2024 at 08:41
Let’s use the lottery example to show the advantages of Bayesian reasoning.
Non-Bayesian Reasoning
Your friend wins the lottery, and you think, “Wow, the probability of winning is 1 in 1 million. They must have cheated!”
Bayesian Reasoning
Let’s apply Bayes’ theorem:
Assign a prior. Cheating the lottery is hard. It’s very uncommon. So, let’s assign a Prior probability (before the win): P(cheating) = 0.0001 (0.01% chance of cheating), P(not cheating) = 0.9999 (99.99% chance of not cheating)
Simplified likelihood fnc:
Likelihood of winning given cheating: P(winning|cheating) = 0.5 (assuming cheating does not guarantee a win but increases the odds from 1 in a million to 50%).
Likelihood of winning given not cheating: P(winning|not cheating) = 0.000001 (1 in 1 million chance of winning fairly)
Using Bayes’ theorem, we update our probabilities:
P(cheating|winning) = P(winning|cheating) * P(cheating) / [P(winning|cheating) * P(cheating) + P(winning|not cheating) * P(not cheating)]
= 0.5 * 0.0001 / [0.5 * 0.0001 + 0.000001 * 0.9999]
= 0.033
P(not cheating|winning) = 1 – P(cheating|winning) = 0.967
Going through the excersize of quantifying things based on educated guesses (prior knowledge and likelihoods) results in a more accurate probability: there’s only a 3.3% chance your friend cheated, and a 96.7% chance they won fairly.
Bayesian reasoning helps us:
Update our probabilities based on new evidence (the win)
Incorporate prior knowledge (the rarity of cheating)
Provide a more nuanced answer than a simple “they must have cheated”
The process of going step by step using educated guesses forces us to account for things like the difficulty of cheating and makes everything transparent.
Your friend wins the lottery, and you think, “Wow, the probability of winning is 1 in 1 million. They must have cheated!” This provides us nothing transparent regarding how you arrived at that conclusion. The second, we can see how you quantify the difficulty of cheating, the odds of winning with and without cheating, and how you combined those things to produce your posterior probability.
This is is why the process is not useless.
19. August 2024 at 09:39
Student, You said:
“By inverting the conditional probabilities, Bayes’ Rule enables us to make probabilistic statements about the cause, given the observed effect.”
Yes, and I cannot even imagine any other rational way of doing things.
21. August 2024 at 08:32
Student,
First of all, I am not the one that needs convincing. With millions of people buying lottery tickets, someone is bound to win even though the chance of anyone winning is really slim, but it is meaningless to ask why this particular person ended up winning the lottery.
Secondly, I agree Bayesian reasoning could be useful, but only in cases where the process/ experiment is repeatable, such as using Bayesian models to predict how Covid could spread or to determine which Covid patients could be most at risk.
More troublingly, it seems those people are trying to prove, based on Bayesian reasoning alone, whether Covid originated from lab leak.
By right, Bayesian reasoning should serve only as a guidance to concentrate one’s resources (say on Covid patients which your model shows most likely to be at risk, or which part of the sea to look for a missing airplane).
21. August 2024 at 20:39
Come on man.