Is Noah Smith a Bayesian?
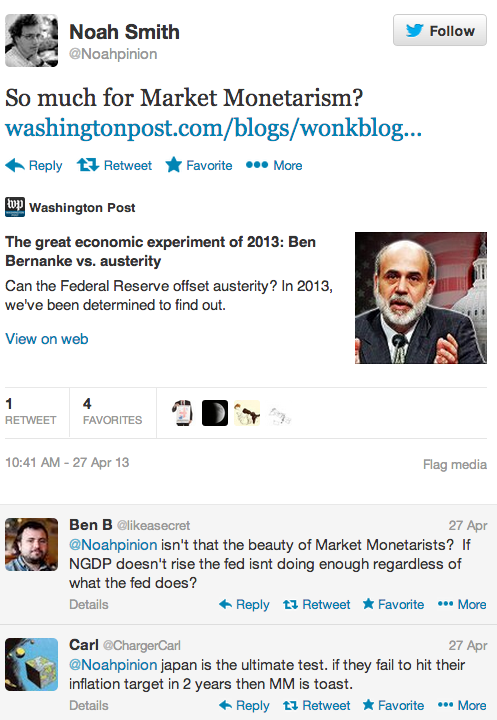
W. Peden sent me this tweet from last April:
Let’s get the two silly comments at the end out of the way first. If the Fed adopts NGDPLT then they’ve “done enough,” and I’ve consistently argued that unless they do more Japan is likely will fall short of 2% inflation (excluding the sales tax bump.)
Of course the beauty of tweets is that they are so short, and hence Noah is free to deny that he was endorsing Mike Konczal’s view that this was a sort of test of market monetarism. I think most readers of Noah’s tweet would assume that he linked to the column because it actually had something interesting to say. And remember, Noah seems to believe that it doesn’t matter what you meant to say, it matters how people read your posts. The reader is never wrong; it’s always the writers fault. I read it as an endorsement, so as far as I’m concerned that’s all that matters. What Noah intended is completely irrelevant.
So I’m going to assume Noah did think that this was a sort of test of MM. And now that the results are in, and the economy performed almost exactly as MM’s predicted and very differently from what Keynesians expected, how does Noah update his priors? This is from a comment section:
For what it’s worth, my prior – that neither fiscal nor monetary policy has a big effect – has been strengthened by events in the U.S., though Abenomics is causing me to slightly question that.
I would have hoped that it would have a more favorable view of MM. Suppose we had “lost?” Doesn’t his tweet suggest that it would have been “so much for market monetarism?” I then asked him to clarify whether he meant real or nominal GDP, and he responded:
I meant no real effect, but I wonder about nominal effects too…
In most models money is neutral in the long run, and hence has nominal effects. I suppose there are ultra-Keynesian liquidity trap models where money has no nominal effect, even in the long run. But in those models fiscal policy is really powerful. So I’d be interested in seeing Noah’s model here. Maybe I’m reading too much into this, as perhaps the key term is “big effect.” In any case, I’ve been quite disappointed to see the blogosphere response to The Great Market Monetarist Experiment. But I can’t say I’ve been surprised.
BTW, here’s a Smith post on Bayesian reasoning:
There has been much discussion lately concerning the word “derp” and its appropriate usage. For example, Josh Barro used the word to describe conservative bigmouth Erick Erickson, and Paul Krugman used it as well. This prompted a primer on the history of the term, followed elsewhere by the usual hand-wringing by self-appointed cultural policemen annoyed by the word.
Now, I myself have used the word “derp” quite a lot. Possibly more than any other pundit I know, with the exception of Dave Weigel. But in any case, not only do I consider myself an expert in the use of “derp”, I also have a very precise idea of what “derp” means, and how it should be used. I think “derp” is incredibly useful as a term for an important concept for which the English language has no other word.
It has to do with Bayesian probability.
Bayesian probability basically says that “probability” is, to some degree, subjective. It’s your best guess for how likely something is. But to be Bayesian, your “best guess” must take the observable evidence into account. Updating your beliefs by looking at the outside world is called “Bayesian inference“. Your initial guess about the probability is called your “prior belief”, or just your “prior” for short. Your final guess, after you look at the evidence, is called your “posterior.” The observable evidence is what changes your prior into your posterior.
It’s a long post, but I think you see where he’s going. I certainly won’t call Noah a derp. Partly because the tweet and blog comments are far too vague, and partly because he doesn’t seem at all like an ideologue. Instead, I’d be very interested in knowing what Noah thinks of a Nobel Prize Laureate who says that 2013 will be a test of market monetarism, and when the results come in exactly as the MMs predicted says that no real test is possible, because other things are never equal, but doesn’t use that “ceteris isn’t paribus” reasoning when using single data points to criticize his ideological opponents. Perhaps Noah will do another post on derps, to fill us in.
PS. As I said earlier, I didn’t think 2013 was a good test of MM. (There is no “wait and see” in macro.) What disappointed me is that lots of other people did think it was a test, were all set to pounce on us when they thought we’d lose, and then said “nevermind” when we won.
Tags:


7. January 2014 at 08:41
Noah gets closer than Krugman. If you click through to his whole post, he thinks that “derping” is “the constant repetition of strong priors.”
I still think it depends. To use my example from the Krugman bit, if I inspect a coin and find it apparently normal, I am going to predict that the chance of any given flip coming up tails to be about 50%. If you announce that you’ve flipped a coin 10 times and gotten tails 80% of the time, I am not going to discount my prior belief by much.
(There’s a chance I’m missing something about that coin or your flipping technique, and that chance inceases the more your flipping experience deviates from normal, but frankly, not by much).
So if you have been betting your mortgage on a coin flip, I’ll tell you that you shouldn’t. And if you’ve won four times and propose to go 16-tuple or nothing, I am still going to advise you not to, and my repetition is not a “derp” – my prior responds to your new evidence.
Noah’s point seems to be that under Bayesian analysis, people who find new evidence unconvincing should shut up and allow people who do find new evidence convincing to proceed unimpeded. I’m not sure that really what Bayes said, but I’ll grant, I’ve never read him in the original, so Noah’s formulation does slightly increase my internal probability of that being true. (Still well below 0.1%, though).
7. January 2014 at 08:50
i may be wrong but i thought derp referred to statements, comments, ideas, etc and not people. so the tweet and comment would be derp but not the author, i think
7. January 2014 at 08:54
After half an hour of reading about the difference between Bayesian analysis and frequentist has caused me to update my beliefs as follows:
1) I probably don’t know what I’m talking about, to the point where the question of whether Cochrane, Smith, or Krugman are Bayesians is not intelligible to me.
2) To the extent that the alternative to Bayesian analysis is frequentist analysis, then I suspect that the vast majority of the world is made up of intuitive Bayesians, to the point where advising someone to be Bayesian is superfluous. Either they are sufficiently sophisticated at math that they understand randomism’s limitations and deploy it defensively, or they are basically Bayesian.
7. January 2014 at 08:56
J Mann: That is not how bayesian thinking works. Imagine your example, you inspect the coin and the coinflipping process and then suppose that you think that there is some probability that the coin is normal and some probability that the coin or the overall coin-flipping process is rigged. Now you see that 8 out of 10 flips were tails.
How does your theory fare? You have to update your theory. It is now more likely that the coinflipping process is rigged and that the coin is not fair.
Imagine you do it the other way around. You cannot inspect the coin or the coinflipping process. You can do a naive assumption that there is 50% chance of the coin being rigged and 50% chance of the coin being fair. Now every flip gives you some information that changes your priors. If after million coinflips you see very, very close to even distribution of both results, this means that probability of the coin being fair is very high.
7. January 2014 at 09:20
JV, thanks. Can I lay out my understanding so you can explain where it’s wrong?
As I read the difference, the Bayesian brings in outside knowledge – he gets to inspect the coin, consider whether the source of the coin has a motive to supply a rigger coin, etc.
Under that analysis, if a coin flip came up tails four times in a row, I know that the probability of that happening under normal circumstances is about 0.5^4.
Contra that, I can assume a rigged coin might have a probability as high as 1, depending on how it was rigged. (Simplest example, someone palmed the fair coin and substituted a coin with 2 tails).
If I knew the probability of starting with a rigged coin versus starting with a fair one, then I could calculate the Bayesian probability of the coin being fair versus rigged after each observation.
Since I don’t, I start with a rough intuitive sense of the initial probability. Was the coin supplied by either of the parties to the bet? Did either party have a chance to substitute coins? Who is doing the flipping?
In my example, unless MY FRIEND is the one who rigged the bet, then either (1) it’s almost certainly a fair coin and he should stop playing double or nothing while he’s ahead, or (2) the game is rigged by the other party, who is hustling him and he should quit while he’s ahead. Either way, I’m giving him the right advice. The relative probability that I assign to (1) versus (2) will depend on my priors, and (2) will increase with each flip, but maybe not appreciably.
– Am I right so far or missing something?
Let’s say I obtained the coin from my pocket and I am doing the flipping, so the only serious possibilities of a rigged coin are that (a) I am the victim of a giant conspiracy that seeded my pockets with rigged coins, or (b) someone has rigged the game through a means that I can’t imagine. Those are both possibilities, but they’re so remote that the Bayesian updating after four tails in a row won’t affect the probabilities by a number large enough for me to express.
– Is that right too?
If that’s Bayesian thinking, then I think almost everyone is a naive Bayesian.
7. January 2014 at 09:33
This post makes it sound like “Bayesian” is some sort of a pejorative.
http://xkcd.com/1132/
7. January 2014 at 09:34
Since you are responding to other blog comments on the test or non-test of MM this year, I’d like to see your response to Simon Wren-Lewis’ Mainly Macro Post on Jan 6th “Monetary versus Fiscal: an odd debate”
7. January 2014 at 09:43
I think that Scott understands Krugman to mean that “Bayesians” update their internal probablity estimates based on observed data, and non-Bayesians don’t.
And as I said, I don’t know what I’m talking about, so maybe both Scott and PK are right.
But it seems to me that everyone updates their internal probability estimates based on observed data – the key question is HOW MUCH you update your probability estimates, and that depends on your prior beliefs about the situation and your observations.
7. January 2014 at 09:44
Ps – the XKCD explained wiki for that strip has been my primary resource for what little understanding I do have. 😉
7. January 2014 at 09:52
J Mann: Yes, what you say seems right to me. The main difference between “bayesian thinking” and “regular thinking” is that you do not defend your pet hypothesis. There is just a hypothesis and then there is evidence. Evidence either makes hypothesis stronger or weaker.
So if you have hypothesis that the coin is fair but you see 8 out of 10 flips ending as tails, you do not go defending your hypothesis on the ground that this result is perfectly normal and possible even with your hypothesis describing how things are.
It is better to imagine that when trying to explain some phenomenon you have to divide some finite probability mass (100%) to ALL possible theories. Every piece of evidence, every new piece information shifts this probability mass assigned to different theories based on how their predictions fit the evidence.
So if you say: “My theory predicts 1% chance of elevated inflation in next 5 years compared to other theories” then when evidence comes out and no elevated levels of inflation were observed, then hypothesis #1 has to surrender some precious probability mass to competing theories – even though there was only a low chance of such an event happening. You don’t go around defending your pet theory by saying that this test means *nothing* because well, there was *only* 1% chance of it happening anyways.
It is also why when trying to prove some theory it is good to produce some specific and strong prediction. Meaning only small number of theories make that prediction and the result is very different from all other theories. The other side of this principle is that any theory that explains *everything* (every possible outcome of evidence) it in fact explains *nothing*.
7. January 2014 at 10:11
J Mann: “But it seems to me that everyone updates their internal probability estimates based on observed data”
Yes, that is what is supposed to happen – no matter how strong your priors were and how weak the evidence is, you should make your “bayesian update”. The Krugman does not do anything like that. He declares that the test of his own devise was not valid because of unspecified “other stuff”
This is exactly how you do not make prediction. Imagine you say thing like this:
“This year economic growth will be a disaster and if so it supports my theory. If it is not disaster then it is some “others stuff” and it still supports my theory”
You simply cannot hedge predictions like this. If you say that your theory supports some evidence and also its negation, then in effect you predict everything and so you effectively make no prediction.
If you make the other part of your “prediction” about other stuff only after evidence is observed then it is pure and simple dishonesty which should be rightfully scorned in better circles.
7. January 2014 at 10:40
Thanks, JV, I really appreciate your patience.
It seems to me that the problem with trying to separate people into Bayesians and non-Basians is that even to a Bayesian, some observations are so worthless as to actually have zero impact, and others have so close to zero impact that one might say zero in normal conversation.
So if I’m very concerned in 2009 that we might see the catastrophic nuclear weapons, and four years later, no one has used one, but I stand by my prediction, I might mean “four years of observation produces such a small change in my internal assessment that it’s effectively zero,” or I might mean that the change is actually zero. I guess I’m being optimistic when I assume that people actually apply an inferential process similar to explicit Bayesian thought, then simplify it at the conscious level or for communication.
In this specific case, if you grant Krugnan the greatest possible benefit of the doubt, then if he had known of the “other stuff” ahead of time, then his model would have predicted this outcome ahead of time, and the outcome therefore tends to increase his confidence in his model. (There must also be an outcome between confirmation and negation that causes him to maintain the exact same probability, but I can’t do the math.) If you’re a little more plausible, then what he means is that the data observation is so uninformative as to have almost no impact on internal probability, to the point that it’s unrewarding to do the work necessary to determine which direction to change his beliefs or by what minuscule amount.
But if you’re that generous, the. Krugman’s criticism of Cochrane also fails, and for the same reason.
7. January 2014 at 10:42
“”But it seems to me that everyone updates their internal probability estimates based on observed data”
Yes, that is what is supposed to happen”
I am not sure every agrees. They teach the frequentest approach to the “the gambler’s fallacy” to every high school student.
That is if a coin flip comes up heads 5 times in a row, what is the chance that the next flip is a head.
Frequentist 50% — it is still a coin.
“Gambler” 50% — the coin may be rigged.
7. January 2014 at 10:51
“New Research Says The Subprime Crisis Would Have Happened Even Without Predatory Lending”
Read more: http://www.businessinsider.com/predatory-lending-subprime-crisis-paper-2014-1#ixzz2pjxjsaKJ
7. January 2014 at 11:02
Oh, don’t know what happened there.
The gambler’s fallacy.
If a coin flip comes up heads 5 times in a row, what is the chance that the next flip is a head.
Frequentist 50% “” it is still a coin.
“Gambler” 50% — they coin may be rigged.
7. January 2014 at 11:03
somthing odd is going on… what I am writing is not what is posting.
7. January 2014 at 11:06
J Mann: No problem. If you are really interested in this whole Bayesian thing I strongly recommend reading what Eliezer Yudkowsky has to say about it here: Great stuff: http://yudkowsky.net/rational/technical/
I even suspect that much of this Bayesian talk in a way originates from him as I know that some econ bloggers follow him (Scott Sumner mentioned him a few times and he even comments her from time to time).
7. January 2014 at 11:09
Jim, He seems to believe that monetary policy is not very effective at the zero bound. I think it’s still highly effective. On the other hand it’s possible that central banks would do less at the zero bound, for fear of unconventional measures. But one can also construct scenarios where they do more, and the fiscal multiplier is negative. I’ve discussed those scenarios in other posts.
I’ve never argued that the multiplier is definitely zero, just that this is a benchmark to start the analysis, and the burden of proof is on those who think it is positive. And not just positive, but economically significant. I agree with Noah that there isn’t much evidence that fiscal stimulus can have a big effect (where monetary offset is possible–not Greece obviously), although I’d never rule out the possibility that it might have some effect.
Travis, That headline is exactly what I would expect. It seems far-fetched that predatory lending along could explain the crisis.
7. January 2014 at 11:14
Everyone, A brief comment on the coin flip. If I pull a coin out of my daughter’s piggy bank, and it looks normal, I’ll have a pretty strong prior it’s not rigged. Five heads in a row wouldn’t change that much. If I observe a magician in a nightclub flipping a coin, my prior will be very different. Context matters.
So I agree with J. Mann.
7. January 2014 at 11:26
Dear Commenters,
If I attend this goldbug conference in Austin, what questions should I ask???
http://www.jsmineset.com/2014/01/02/austin-texas-qa-session-confirmed
7. January 2014 at 12:12
Scott: “Everyone, A brief comment on the coin flip. If I pull a coin out of my daughter’s piggy bank, and it looks normal, I’ll have a pretty strong prior it’s not rigged. Five heads in a row wouldn’t change that much”
It depends. It does not change relative to what? If you start with really small probability, then experiencing a “1 in 30” event could significantly increase the chance of the event (I am too lazy to do an actual math)
This is actually the whole point of Bayesian reasoning. In general people tend to stop paying attention to large probabilities. For them 99% probability of an event is basically the same as 99.99% probability of an event and it is synonymous to saying “I am pretty damn sure”. But it is not the same thing! You just increased the probability of low-probability event by a factor of 100.
Another way to say is that imagine that you put money where your mouth and actually put a bet on that fact that the coin is fair given your fairly confident priors. Now even after few flips of coin you may start sweating, is it possible that you mispercieved the risk by such a huge factor? If so you may lose quite a lot.
7. January 2014 at 12:26
Hahahahahahaha run for your lives!
Shadow Government Stats:
HYPERINFLATION 2014″”THE END GAME BEGINS
HYPERINFLATION 2014″”THE END GAME BEGINS
HYPERINFLATION 2014″”THE END GAME BEGINS
HYPERINFLATION 2014″”THE END GAME BEGINS
January 7th, 2014
http://www.shadowstats.com/article/no-587-hyperinflation-2014-the-end-game-begins
7. January 2014 at 13:11
TravisV,
My favorite Shadow Stats price index is the Shadow Stats subscription price itself.
Currently, an annual subscription costs $175:
http://www.shadowstats.com/subscriptions
eight years ago, an annual subscription cost … $175:
http://gyroscopicinvesting.com/forum/index.php?topic=1425.0
7. January 2014 at 13:32
The most interesting reading (at least for me) in the past few days, from a number of perspectives, has actually been the comment thread of this article:
http://www.pieria.co.uk/articles/how_to_confuse_with_mathematical_models
Basically Frances Coppola got caught being extremely rude and rather than apologize forthrightly has chosen to make even more rude comments on Twitter.
I almost commented on the econometrics but the other commenters already addressed all of the issues better than I could. So it also makes for some interesting reading from an econometric perspective.
Costas Milas has written a response (to the substantive points):
http://www.pieria.co.uk/articles/more_on_why_the_governments_policy_in_dealing_with_the_rising_debt_burden_in_the_current_low_growth_environment_is_indeed_justified
In my opinion the empirical evidence on whether public debt leverage causes low real growth or low real growth causes public debt leverage is very mixed. Milas’ results may be true for the UK over 1831-2013 but I doubt that they are true for all countries or for all time periods.
7. January 2014 at 13:41
Evidently Piera has pulled Milas’ response (the plot thickens). You can also find it here:
http://blogs.lse.ac.uk/politicsandpolicy/archives/38813
7. January 2014 at 14:11
Noah Smith’s new list of blogging heroes:
http://noahpinionblog.blogspot.com/2014/01/heroes-of-blogging.html
My response in the comments section:
“I don’t understand: why exactly did you exclude Scott Sumner from this list? He’s a far bigger hero than any of these other people. He was the only one insisting “The Fed is not out of ammo!” when it really counted in early 2009.”
7. January 2014 at 16:56
Doug M,
Re: the XKCD comic on Bayesian statistics…
http://www.explainxkcd.com/wiki/index.php/1132
“The final panel is a tongue-in-cheek reference to the absurdity of the premise. If the sun did explode, he won’t need to pay out the bet because the Earth and everyone on it would be destroyed. But if it didn’t explode, then he’ll win $50.”
But literally the Bayesian just doesn’t think the new evidence (which is suggestive of Sol going nova) is strong enough to overcome the prior odds.
7. January 2014 at 17:40
OT but maybe not…is money “long-term neutral”?
What if an expansive monetary policy encourages capial investments? Conversely, did tight money in Japan adversely impact island growth over 20 years?
Is not 20 years the long term?
If economic models do not anticipate accretions to capital or changes in human behavior…
7. January 2014 at 18:52
Benjamin,
I think “long term” depends on how sticky wages are. In Japan, they are pretty darn sticky.
7. January 2014 at 18:57
YOU ARE AN IDEOLOGUE SUMNER!
i·de·o·logue
ˈīdēəˌlôg,-ˌläg,ˈidēə-/Submit
noun
1. an adherent of an ideology, esp. one who is uncompromising and dogmatic.
——————-
An adherent of an ideology? What’s an ideology?
i·de·ol·o·gy
ˌīdēˈäləjē,ˌidē-/Submit
noun
1. a system of ideas and ideals, esp. one that forms the basis of economic or political theory and policy.
——————–
Can you please stop throwing that term around like it’s a pejorative already? An odeologue is one who adheres to an ideology, and Market Monetarism is an ideology.
IT’S NOT WRONG OR BAD OR A FLAW TO BE AN IDEOLOGUE.
Gee whizz.
7. January 2014 at 20:08
@Geoff. There’s a difference between definition and connotation.
con·no·ta·tion
/ËŒkänəˈtÄSHÉ™n/
noun
1. an idea or feeling that a word invokes in addition to its literal or primary meaning.
7. January 2014 at 21:41
Shadow Government Stats:
HYPERINFLATION 2014″”THE END GAME BEGINS
I’ll bet them $50 dollars that they are wrong. Payable in 2016, when we’ll know for sure.
Oh, heck, make it $5,000. Unless they are so sure of themselves they want to go for more.
7. January 2014 at 21:43
Kevin Dick:
“In addition” doesn’t apply here, because “in addition” would presume the definition is being properly used.
Notice the definition you cited doesn’t say “despite” or “in contradistinction with” or “instead of”.
7. January 2014 at 21:44
Geoff, now look up the meaning, in psychological behavior terms, of the word: “projection”.
7. January 2014 at 21:45
Jim Glass,
Even if Shadowstats is right (which they likely won’t be, but just for the sake of argument), the likely response would be “Even a broken clock…”
7. January 2014 at 21:46
Jim Glass:
“Geoff, now look up the meaning, in psychological behavior terms, of the word: “projection”.”
That is an excellent interpretation of Sumner’s use of the term “ideologue.”
7. January 2014 at 23:44
dtoh:
I think it must go deeper than that. Sure sticky wages, but that would clear up after five to seven years, no?
But by then, you have had five to seven years of depressed output, and depressed capital investment due to a depressed outlook. What started off cyclical, starts to look secular.
Then the problems of real estate, in which loans are extended in nominal terms. If real estate is depressed, you have serious problems in your banking sector. So they pull in their horns.
No, one cannot just print money and have higher living standards, I understand that.
On the other hand, a monetarily induced recession, and then persistent tight money thereafter, seems to be strong enough poison to keep the economic patient under for decades.
For me, 20 years is the long run. People do not live much beyond 70 years, and our working life and ability to accumulate capital is less than that.
8. January 2014 at 01:47
Cthorm: Actually I do not think that “overcoming” priors is the most important lesson from Bayescraft, at least not in this manner. Many times the point where you change your priors is nothing “special”. You may have just mispercieved your previous priors anyways, right?
It is better to see it when using the parable of 5 coinflips ending tails. Let’s say that you think that there is only one in a million chance that the coin is rigged. So how many coinflips do you require to change your priors?
So we have 5 tails in a row. Nothing “dramatic” your confidence of the coin being fair changed from 99.9999% to 99.997%. You are still pretty damn sure. Another batch of 5 coinflips turned tails. Ok, the probability changed from 99.997% to 99.9%. Still pretty sure. Another 5 flips
and the chance is still 96.67%. Even after 15 consecutive tail flips you are quite confident in your hypothesis. Your prior is not changed. But now the “dramatic” part starts to happen (at least to ordinary man).
Coin flip 16 tails > 93.45%
Coin flip 17 tails > 86.89%
Coin flip 18 tails > 73.79%
Coin flip 19 tails > 47.57% ………… PRIORS CHANGED
But the 19th flip is not “magical somehow”. It is wrong to say that *nothing* changed up until 19th flip. On the contrary, the theory had to go a long and dramatic way only to get to a spotlight. There were huge relative changes in plausibility of theory. Every batch of 5 flipcoins its chance to “win” increased from 1:million to 1:30,000 to 1:1000 etc.
It required a lot of work to even get to that point. And the hardest part of being the “bayesian” is to realize that most of the work when promoting a hypothesis needs to be done before the glorious finish so that the evidence satisfies your priors.
The point is that strong priors are not as “safe” as you think. If Krugman really thinks that there is only one in a million chance that Market Monetarism is right and his test was a good one similar to batch of 5 coinflips, then it requires just 3 another tests like that in order for him to change his views.
Plus there are some other things. For instance there is the fact that he even bothered to construct the test in the first place for something he really things is not true may mean that his priors may have been weaker than 1:million. But it also means that now when the first test was passed he has much more incentive to immediately follow up with another test to falsify this new theory. It does not make sense to say “other stuff” and then refuse to go down the rabbit hole in fear for his pet theory being wrong.
8. January 2014 at 05:43
JV, You said;
“It depends. It does not change relative to what? If you start with really small probability, then experiencing a “1 in 30″³ event could significantly increase the chance of the event (I am too lazy to do an actual math)”
I don’t follow this. If I start with a 1/billion probability of it being rigged, a 1/30 outcome won’t change that significantly.
Mark, That shadowstats comment is really funny.
Ben, Good point, it doesn’t become fully neutral until the very very long run. But it’s approximately neutral in the long run. All of these models are approximations of reality.
8. January 2014 at 06:00
Scott, it looks like JV did the math for one in a million and you guys agree. (IMHO, most non economists or mathematicians would probably change their intuitive probability model more than the math would suggest because people tend to overestimate miniscule risks, but the point’s sound).
8. January 2014 at 06:22
“Beijing should scrap the GDP Target”
http://on.wsj.com/1gDHwgt
I agree. They should target NGDP!
8. January 2014 at 07:53
Scott: If you start with prior probability of “1:billion” than after 5 coin flips it changes to “1:30 million”. The chance of coin being rigged increased by factor of 30. That is quite a lot.
You may say “5 consecutive coinflips don’t make me change my view”. No maybe it is not evidence powerful enough for you to “overcome” priors. But it should make you less confident about coin being fair and more confident in coin being rigged – by factor of 30!
Or to put it differently. With your 1:billion prior probability of the coinflip being rigged you require 30 coinflips to switch your opinion. After 5th coinflip ending tails you are 16,6% percent on your target to prove you wrong. It takes “only” another 25 flips to turn your view around. Maybe your daughter keeps a rigged coin in her purse to do magic tricks for her friends?
This is the key. You have to say “given that I just saw 5 consecutive tails I am only 25 flips away to make me change my view”. You don’t say “Ah 5 consecutive tail flips is nothing, it is perfectly expected given my very strong priors so I can safely stop tossing the coin”. Because here another 5 such *nothings* will make you change your claim. And you have to be prepared to do that. And more importantly, you have to be prepared to increase the chance of this happening flipcoin-by-flipcoin.
8. January 2014 at 08:55
JV – Scott says that 5 flips in a row wouldn’t change his views of a coin he had reason to believe was fair “MUCH.”
I think you guys have been agreeing for some time.
Here’s my thought – IMHO, it’s constructive to combine some “rational ignorance” concepts with Bayesian analysis. To a normal person making decisions in a lifetime the difference between 1 in a billion and 1 in 30 million is close enough that it’s not rational to do the work to distinguish them.
My assumption is that the risk of catastrophic failure on any given roller coaster ride in the local amusement park is somewhere between 1 in a million and 1 in a hundred million, but I’ll acknowledge there’s a possibility that I’m off by another order of magnitude on even that rough estimate. Since that distinction isn’t relevant to my decision to ride or allow my family to ride, I don’t do the work.
Now, it’s absolutely true that when I read about an amusement park accident, I raise my internal risk estimate by a little. How much is a product of an internal guestimate about how likely I think it would be that an accident would be reported in the news sources I read and how many rides occur a day, but because I don’t do a literal calculation, the result has so far been “too remote to prevent me from riding the roller coaster,” and “too remote to calculate in more detail.”
So it looks like I’m not updating my prior, if my prior is stated at the level of generality as “roller coasters are worth the remote risk involved.”
In fact, you’re right that if I read about enough accidents, at some point, I will decide that the risk was higher than I thought, to a point where I should reduce our roller coaster exposure.
I think that makes me, and just about everyone else I know of, an intuitive Bayesian, so I don’t buy Krugman’s apparent idea that people who haven’t read Bayes or Laplace or Silver don’t know to update their ideas.
To go back to my first point, I don’t think I buy Noah’s point that me repeating my priors is “derp-ing.” If he presents me with someone who says they get relief from faith healing, I might say I’m not convinced because placebo effect, my assumptions about health care research tending not to leave ripe fruit unpicked, anecdote not equaling data, etc. If he presents me with ANOTHER faith-healed individual, I’ll probably say the same thing. You’re right that if he finds enough of them, at some point I’ll tip into curiousity. I think that makes me Bayesian, not a derp.
8. January 2014 at 09:27
J Mann: Ok, my point is that with probability you cannot say “MUCH” in absolute terms, like for instance 10% is much but 0.1% is a little. This is your intuition playing with you.
Bayesian logic is all about being precise. Imagine there is an event #1 that has “true” probability of 1% happening and there is an event #2 that has “true” probability of 50% of happening. If you are mistaken by 0.5% point on both accounts you are wildly inaccurate in case #1 case and only slightly inaccurate in case #2.
Or imagine that every assesment of every probability you make a bet that is leveraged so that you can calculate it comparing to a payoff of an event with 50% probability everybody is comfortable thinking about (because this may be the threshold where we change what we say). So if you say that something has 50% chance happening and you bet $10 on it while if there is something you say it has only 5% chance of happening you should be fine betting $100 on it and so on. You try it few times and you find out that once you get pass some threshold your estimates start to be way off.
Now I understand what you are saying with roller-coaster example. All I am disputing is what it means MUCH. It may make a lot of qualitative difference. For instance imagine that you just pick random coin from your purse and you toss it just because you kill time while relaxing and thinking about something else. Then you notice that it came up as tails five times in a row. Your interest is maybe picqued and if the outcome would be different you may have put the coin aside and go about what you wanted to do. But now you go about tossing the coin a few times more to see what is going on.
This is Bayesian thinking on some subconscious level using pattern-discerning capabilities of our brain. A hypothesis of rigged coin was not even considered before the first 5 coinflips happened. This idea was promoted among competing ideas that may have caought your attention by a simple fact of how “rare” it is given your idea how coins should work. What happened is that after bayesian update this idea was promoted to your attention. It “won” a lottery, it has HUGE impact compared to alternative universe where the coinflips were “ordinary”.
Or to put in in another way, if 1:billoon chance requires 30 bits of information (2^30 is approximately 1 billion) then first 5 bits are equally “important” as last 5 bits in getting the hypothesis promoted in your eyes. You should be able to discern that such a thing is happening before your eyes so that once something gets your attention you stick to testing it not dismissing it. So when you already saw 29 coinflips and take a look at how the 30th flip ended you don’t go from “nothing to see here folks, coin is fair” to “wow the coin is rigged” but you realize that this was just another building block just like 29 before it.
8. January 2014 at 09:30
JV, I don’t think I said it was nothing, I said it was very trivial. And it is. You said:
“Scott: If you start with prior probability of “1:billion” than after 5 coin flips it changes to “1:30 million”. The chance of coin being rigged increased by factor of 30. That is quite a lot.”
No, it’s not a lot. It’s 970/1,000,000,000, which is so trivial it wouldn’t even be worth thinking about. Not “nothing,” but trivial.
8. January 2014 at 09:42
Hmmm. I don’t know whether Bayesian analysis requires one to do the math on all the probabilities in one’s life or not.
That’s a good insight, and my understanding of the Silver book is that he’s a sabermatrician who argues that actually doing the math on your intuitive perceived probabilities helps flush out some misconceptions.
If Krugman and Scott argue that a good Bayesian has to quantify probability foundations and updates, then I guess I need to go read Silver to see if I understand what everyone is talking about. Thanks for sticking with me. 😉
8. January 2014 at 10:24
What if you later discover that your daughter bought that piggy bank at the magic shop?
8. January 2014 at 11:11
woot i made it into a Sumner post!
8. January 2014 at 13:30
Noah replies, saved by the question mark:
http://noahpinionblog.blogspot.com/2014/01/bad-event-studies.html
8. January 2014 at 13:57
JV,
Your characterization of Bayesian logic is very different from mine. For me the core is inference, not precision. IMO frequentist statistics aims for precision, while bayesians emphasizes the uncertainty.
8. January 2014 at 14:12
There’s a classic George Carlin routine that everyone who drives slower than you is a moron and everyone who drives faster than you is an a-hole.
I’m sure Noah’s conception of Bayesian thought is more sophisticated than comes across in the two blog posts I’ve read, but so far, that’s what he reminds me of.
Everyone who updates their priors less than he does from a given event is a “derp,” everyone who updates them more is a frequentist.
(I know, that’s not fair – he’s in the middle of the bell curve, and the derps and frequentists start pretty far out to the right and left, but still . . . )
8. January 2014 at 15:48
Noah’s response is lame. If the results of 2013 had gone Krugman and Konczal’s way, those two would be writing Market Monetarism’s obituary right now. And Noah probably wouldn’t object much at all.
8. January 2014 at 20:42
“This is uncharitable, but I think of market monetarism as a theory that can only be confirmed, never rejected.”
http://www.arnoldkling.com/blog/macro-experiments/
9. January 2014 at 01:08
Cthorm, Scott: What I want to say by “precision” is bayesian concept of calibration. If you say something has probability 2% but in reality it has probability of 5% then you are poorly calibrated even if the thing happens only “sometimes” and you deem the difference as “trivial”. This is quite a large sin from bayesian logic point of view, you made a large mistage in your judgement.
So even if you change your prediction of some by “trivial” ammount in some intuitive absolute terms, it may be large change in how well calibrated you are. If you say that something has probability of 1:billion but it has probability of 1:million it is the same order of poor calibration as if you say something has 90% of probability of happening and in reality it happens only in 9 times out of 1000 occasions.
I don’t know how else to say what I mean to say. The biggest issue is that ordinary people express strength of confidence by probabilities. 10% maybe translates as “not confident” and anything above 99% translates as “pretty damn sure”. This is not what probability means in bayes-speak. The same goes the other way, saying that I updated my prediction “only” from trivial 0.0001% to still “trivial” 0.001% is a sin.
9. January 2014 at 05:14
JV, I haven’t done the reading, but do Bayes and LaPlace really think people should distinguish between 1 in a million risks and 1 in a billion if the cost benefit doesn’t justify the effort required to make the distinction?
9. January 2014 at 06:00
JV, None of that has any bearing on anything I said. How Bayesians think about these differences is irrelevant. I’m a pragmatist, and all I care about is the pragmatic implications of any change in estimates. That means only absolute changes matter to me, not percentage changes. If some Bayesians think about things differently that’s fine. But my math was 100% correct in Bayesian terms so they have no argument against my logic. If I say Gov. Christie is 238 pounds, and he is exactly 238, it makes no difference if I regard him as fat and someone else does not. That’s all you are disputing, how the change is characterized, not how big it is.
Saturos, That Kling quotation is idiotic.
9. January 2014 at 06:10
J Mann: Depending on where you use it. In a common language I pass these remarks, but since this is a post about Bayesian thinking I thought it is worth mentioning that it really is important.
There is another parable that came to my mind: logarithmic scale. Imagine how loudness of sound is measured. It would like saying that the difference between the tiny changes in air pressure (let’s say -80 dB) and weakest sound that can be heard (0 dB) is “trivial” – no human can tell the difference anyways, right? While difference in loudness between regular conversation (60 dB) and jet engine 100 feet away (140 dB) is “huge” – possibly because such a change can damages your hearing.
So I do not object that people may not know exactly very small probabilities. What I object is that even if they do not know these exact tiny prior probabilities they know the magnitude of the shift. What I object is that somebody says that 80 decibel magnitude shift is “not much” – just because he still cannot hear it. Because maybe another 1 or 2 such “not much” shifts and he can lose his hearing.
So long story short: proper reaction should be:
“Given the evidence I significantly increased plausibility of the theory. It still did not pass my confidence threshold for me to publicly subscribe to it, but everyone who already bothered testing this theory should increase their effort to further disprove it and maybe some other researchers who so far ignored the theory because it was not worth the effort for them may want to reconsider. Anyways it was a big win for this theory today.”
9. January 2014 at 06:32
Scott: No, all I am disputing is that huge relative shift in probabilities has to be recognized as such. To use your example it would be like if your previous assumption was that gov. Christie is 2380 pounds but now you assume that he is 238 pounds and than say “Yeah, he is still fat so not much of a change in my opinion. No practical impact or anything”.
And I am not disputing that this is common pracice of all of us. But since this post is named “is Noah Smith Bayesian” I thought it relevant to comment that it is different. If you are true bayesian you do not hold view of binary outcome like “fat” and “not fat”. Or “I write a blog supporting idea or I don’t”. Doing such stuff is not bayesian, it is what all people do all the time.
Bayesians constantly do updates based on evidence. You try to be well calibrated and simultanously try to better discriminate to get the best possible Bayesian score.
9. January 2014 at 06:39
PS: just a note, advantage of being bayesian is that no matter what your priors are you end up with good results given enough iterations. You don’t ignore evidence just because it did not go over some threshold, you make updates one after another. This works especially well if your priors are not well grounded. That is how you for instance train bayesian antispam engine even if you start up with some totally random weights if you feed it enough information about what is and what is not spam.
9. January 2014 at 07:17
JV, Scott’s playing off this Krugman piece, where Krugman argues that Cochrane isn’t using Bayesian thought because Cochrance continues to believe that there is a significant danger of inflation and catastrophic loss of confidence in US government debt, even though that hasn’t happened in the last four years.
http://krugman.blogs.nytimes.com/2013/12/01/inflationistas-at-bayes/
I love the digression about Bayesian analysis and enjoy the education, but for purposes of this conversation, the right question is probably “what did Scott understand Krugman to mean?”
It’s always hard to figure out what Krugman means, beyond the obvious “Krugman means that Krugman is much smarter and better informed than Cochrane.” But he seems to mean that instead of saying “I still think inflation is a significant danger,” Cochrane should have said.
“I still think inflation is a signifant danger, and although the past four years have caused me to revise my estimate of the danger level by a trivial amount, it doesn’t change my overall point.”
or maybe:
“In 2009, I thought that we had a chance of increasing inflation that followed the following function over time: f(x), and I thought f(x) had the following probability of being true. y” Because f(x) produces fairly low rates in the early years, the lack of inflation in the first four years is not greatly concerning, but compared with the alternative hypotheses, when you do the math, it has lowered my probability estimate to y-z.”
or maybe:
“The last four years are not a good test of my theory because of other stuff.”
9. January 2014 at 08:29
J Mann: Actually if we go back to original post I am with Scott on this one. Noah Smith (and Krugman for that matter) are the ones making bayesian sin. Noah Smith doubly so as he poses himself as understanding and promoting bayesian thinking. Smith endorsed Market Monetarist test back in April, Market Monetarism passed the test perfectly and now he responds that his skeptic priors of validityy Market Monetarism were “stregthened”. This as anti-bayesian as it gets. One is not bayesian by using word “my priors” or “posterior” in a random blogpost.
This whole line of post about bayesianism was spurred by Scott’s notion that some relatively strong evidence “does not change his opinions that much”. I beg to differ on this one from Bayesian point of view – which is all my recent posts are about.
10. January 2014 at 14:26
JV, You said;
“No, all I am disputing is that huge relative shift in probabilities has to be recognized as such. To use your example it would be like if your previous assumption was that gov. Christie is 2380 pounds but now you assume that he is 238 pounds and than say “Yeah, he is still fat so not much of a change in my opinion. No practical impact or anything”.”
That’s an absolutely horrible analogy. Adding 2000 pounds is a huge deal, you get a heart attack. Adding 970/billion in risk is so small it doesn’t change my behavior at all.
You said:
“If you are true bayesian you do not hold view of binary outcome like “fat” and “not fat”.”
You are contradicting yourself. I said no big deal and you said big deal. That’s binary. If it’s not binary then you should let me say “no big deal.”
13. January 2014 at 03:09
Scott: I do not want to argue with you, not like this. As for “not much” vs “much” from bayesian point of view the change of probability has to be compared to what you previously believed.
The lower the probability of a phenomenon the higher the information value it has if happening. Misstating probabilities has huge implications from this point of view and vice versa – how huge a mistake somebody made in bayesian sense can be measured by this. Therefore you cannot escape quantifying the magnitude of this sin.
And no this is not “binary” speaking. Mistating probabilities by an orders of magnitude is huge sin in bayesian thinking. It may not have the same implications in regular thinking, I give you that (like for instance chance of a heart attack or chance of going deaf from loud sound etc.). I was not talking about these things.
PS: thank you for the discussion, I actually have better grasp of what I wanted to say trying to explain it. At this point I surrender as I do not think I can express myself cleared than I have in several examples that I tried to give. Maybe you assumed that I am attacking you even if I was not. Thank you anyways.
13. January 2014 at 05:30
Ok, one last thing as I found that Noah Smith also has some different view of what bayesian change of opinion means. This is just a copy-paste from my response to his post:
Noah: “But notice that Bayesian beliefs depend on your priors”
It may be so, but your priors may be wrong and you should punish yourself more the more confident you were in these mistaken priors. I had this discussion with Scott Sumner and god, it is frustrating.
Ok, lets have this example: you have 3 theories that may explain some phenomena. You need to be more than 50% confident in order for you to publicly subscribe to a theory. Imagine that your priors are as follows: 51% for theory A, 48.99999999999 for theory B and 0.00000000001 % for odd theory C that you deem almost impossible.
Now new evidence comes up that makes you update your priors as in the following 2 scenarios:
1) New evidence supporting theory B appears so that the posterior probabilities are as follows: A – 49% ; B – 51.99999999999% and C – 0.00000000001 %
Since it is now theory B that passed the threshold you make public announcement that effective now you are “completely” changing your opinion and now support theory B. However from Bayesian point of view it is not complete change of opinion. You reduced probability of theory A and B by approximately 4%. We may say that it is not a large change. You made a mistake, but not a large one.
2) New evidence supporting theory C appears. Now it looks like this: A – 51% ; B – 46.99999999999% and C – 2.00000000001 %
Now your public “opinion” did not change much. No bold statements, you still support theory A, right? But this is HUGE, really HUGE from bayesian point of view. You just elevated something from being labeled as “really, really incredibly not likely” to just “not likely”. You made a huge change in your bayesian scoring scale. You should really berate yourself for having such terrible priors.
So Bayesian is something else from what you think. The most useful concept here is that of information entropy, a concept from information theory. This concept can help you measure how “surprising” a change in probability was, how much new information you gained with a new evidence. The point being that the lower the probability of a surprise the larger the information value it has. Promoting low probability even by orders of magnitude means a lot of information was gained. And by this account the scenario 2 has a much larger impact then scenario 1.
20. October 2015 at 05:22
[…] there’s been a wave of posts by Scott Sumner and David Beckworth calling me and others out, saying that the votes are in and it’s a […]
12. November 2015 at 08:36
[…] there’s been a wave of posts by Scott Sumner and David Beckworth calling me and others out, saying that the votes are in and it’s a […]
16. February 2017 at 20:26
[…] You go boy! I’m referring to Noah here. I love this-he calls him out for his ‘small-sample Frequentist Event Studies’ and he’s exactly right. It’s also a nice comeback as Sumner has being knocking Noah as a ‘Bayesian’ lately-in the world of economists these are fighting words: Bayesian! small-sample Frequentist. http://www.themoneyillusion.com/?p=25795 […]