Two examples of low interest rate monetary policies
I’ve done a number of posts comparing New Keynesian and NeoFisherian views on the relationship between monetary policy and interest rates. Here I’d like to illustrate the problem with a picture, as people often have trouble understanding this issue. It’s really hard to not reason from a price change. It’s hard to stop thinking of interest rate movements as a “policy” rather than an outcome.
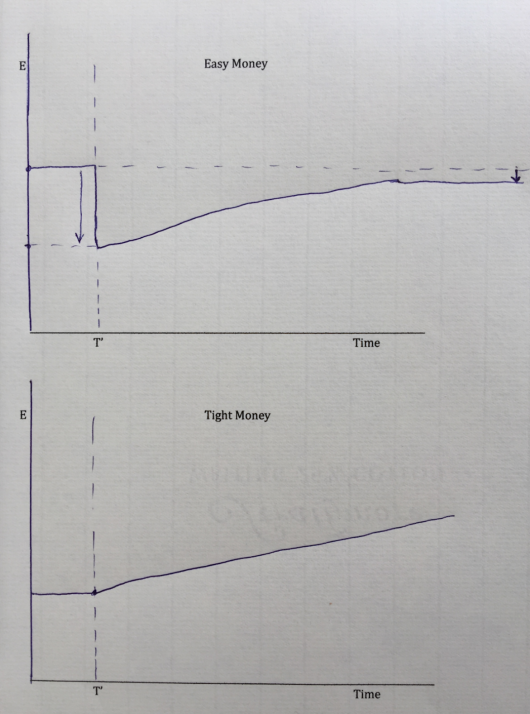
These two graphs show the path of the exchange rate (E) over time, under two different monetary policies. In both cases a higher exchange rate (E rising) reflects domestic currency appreciation. Importantly, both of these examples are “low interest rate policies”, when the central bank reduces interest rates to a lower level than before. But case #1 is an easy money policy, whereas case #2 is a tight money policy:
To focus on the essentials, I’d like to assume that a policy change occurs at time = T’, and that the following movement in the exchange rate is anticipated, once policy has shifted. (The policy move itself was unanticipated beforehand.)
Notice that in both cases, the exchange rate is expected to appreciate after time = T’. Because of the interest parity theory, this expected appreciation means that interest rates will be lower than before the policy change, when the exchange rate was stable and interest rates were the same as in the other country. So from the interest parity theory we know that these two cases are both shifts to a lower interest rate policy.
But now let’s look at the long run impact of the two policies on the level of the exchange rate. In case #1, the exchange rate ends up lower (depreciated) in the long run, despite the near-term expectation of appreciation. Because of PPP, that means the policy is expected to increase the price level in the long run. In other words, it’s an expansionary monetary policy.
In case #2, the exchange rate appreciates in the long run, yielding a lower price level. That’s a contractionary policy.
Because the first case looks so convoluted—a currency that is expected to appreciate over time but still end up lower than before—you might think it represents the “weird and controversial model”. Just the opposite, the first case is the New Keynesian model of easy money, and more specifically the Dornbusch overshooting version. The second more straightforward case reflects the weird and controversial NeoFisherian model. Just looking at the second graph, it’s easy to see how the NeoFisherians are able to get their result from mainstream mathematical models of the economy.
Here’s another way of thinking about the two cases. In case #1, there is a one-time increase in the money supply (and/or reduction in money demand). It reduces interest rates (due to the liquidity effect.) But it also leads to expectations of a higher price level in the long run, due to currency depreciation and PPP. Because prices are sticky in the short run, the effect of easy money is to initially depreciate the currency, not raise the price level in proportion.
In case #2, there is a permanent decrease in the growth rate of the money supply (and/or increase in money demand growth). Because of the quantity theory of money, that leads to a permanent decrease in the inflation rate. And because of the Fisher effect, the lower inflation leads to lower nominal interest rates. And because of interest parity, lower nominal interest rates lead to an expected appreciation in the currency. But you don’t even need the interest parity relationship. By itself, the lower expected inflation combined with PPP leads to the expected appreciation in the currency.
So how does this help us to better understand the New Keynesian/NeoFisherian dispute? It may be helpful to contrast the “highly visible” with the “highly important”. The New Keynesians are focused on the highly visible, while the NeoFisherians are focused on the highly important.
The vast majority of specific, short-term decisions by central banks are better viewed as one-time shifts in the money supply, rather than permanent changes in the growth rate of the money supply. Thus “easy money” announcements often make short-term interest rates fall, even as inflation expectations rise. At the same time, the truly major moves in interest rates over time largely reflect longer-term changes in the growth rate of the money supply (and money demand—in more recent years). Thus the low nominal rates in Japan are primarily due to tight money, not easy money.
Both the New Keynesian and the NeoFisherian models are wrong, as both sides engage in reasoning from a price change. The correct (market monetarist) model says that low rates can reflect easy or tight money, and that one should not draw any inferences about the current stance of monetary policy by looking at interest rates.
If one cannot draw any inferences about the current stance of policy by looking at rates, can one draw any inferences at all? I see two:
1. On any given day, a decision by a central bank to cut rates by more than the market expected is usually (not always) expansionary. It reflects “expansionary intent” and may be viewed as a signal by the central bank of a desire to make policy more expansionary. This is, of course, consistent with New Keynesianism. But it does not mean the current stance of policy is expansionary.
2. When nominal interest rates fall persistently over a long period of time, it is usually (not always) evidence that monetary policy has been contractionary. (This is more consistent with NeoFisherism). But it does not mean that the current stance of monetary policy is contractionary. As usual, Milton Friedman was decades ahead of the rest of the profession:
Low interest rates are generally a sign that money has been tight, as in Japan; high interest rates, that money has been easy. . . .
After the U.S. experience during the Great Depression, and after inflation and rising interest rates in the 1970s and disinflation and falling interest rates in the 1980s, I thought the fallacy of identifying tight money with high interest rates and easy money with low interest rates was dead. Apparently, old fallacies never die.
In America, monetary policy in 2017 and 2018 became a bit more expansionary, despite higher rates.
Tags:


29. May 2018 at 15:41
A nice post. A few remarks:
The Dornbusch overshooting model is an old Keynesian model, in the sense that it has an IS curve in it which relates the level of the output gap to the level of real interest rates. New Keynesian models don’t have these things in it, even if they get an LM curve from somewhere by including money in the model (rather than treating it as an abstract unit of account, a la Woodford). They also have different dynamics – NK models remain stubbornly neo-Fisherian when they are closed on the demand side by LM curves, or equivalently MV = PY where V is an increasing function of the interest rate spread between bonds and money. In the standard NK model, the initial impulse response to a one-time increase in the monetary base is a lower real interest rate but a higher nominal interest rate – the liquidity effect of money is insufficient to also bring nominal interest rates down. Through sufficient ingenuity one can modify the standard model to make the liquidity effect strong enough to produce the “conventional” result (the result in the data, I may add), however.
It is also worth mentioning that neo-Fisherism can be interpreted in several different ways, one of which is the stability of nominal interest rate pegs – more precisely, if the central bank decides to do whatever it takes in terms of monetary policy to keep whatever its policy rate is at a low level permanently, it will end up producing low inflation permanently, rather than the ever-increasing inflation that Friedman foresaw in his 1968 paper. Phrased this way, neo-Fisherism is not reasoning from a price change, although clearly “neo-Fisherism” means different things to different people. This does not have to imply that a one-time reduction in the monetary base, or a permanent reduction in the growth rate of the monetary base, immediately leads to lower nominal interest rates – it can cause, as it did in the early 1980s, an initial increase in nominal interest rates. This is not inconsistent with neo-Fisherism.
The exchange rate movements become quite a bit more complicated (even in a purely Fisherian setting) if you abandon uncovered interest parity (which fails in the data) and perfect foresight, and replace it with, say, an AR(1) model for the log of the nominal discount factor (the kind of thing we often use in bond pricing models, like the simple discrete time Vasicek model) and rational expectations. In this formulation, the exchange rate is a signal of the *level* of the discount factor, while the interest rate is a signal of the expected *growth*. So, in fact the Fisher effect can accomodate many kinds of stories – one can produce a correlation very close to unity between the level of bond yields and the level of the exchange rate in the short run, even though in the long run the Fisher (uncovered interest parity) effect dominates.
Following up on the last paragraph, a natural implication of the ratex framework is that interest rates are even less useful as indicators of the stance of monetary policy than this post suggests, since the models in this post are all perfect foresight models. In the presence of uncertainty about the future, the risk-free interest rate only encodes one dimension of monetary policy (it pins down the expected value of the nominal discount factor, while the stance of monetary policy depends on the entire distribution of both real and nominal discount factors), while to fully understand the stance of monetary policy in a complete market one needs to know the discount factors themselves, or the prices of all Arrow-Debreu securities on the market. Markets are incomplete in the real world, but the basic point that interest rates only capture one dimension of a high dimensional monetary policy structure remains true.
I’m more of a fan of the fiscal theory of the price level, in which most of the same points about trying to use nominal interest rates as a guide to the stance of monetary policy remain true.
29. May 2018 at 17:11
John Cochrane has a post up explaining how recent history proves he is right in his fiscal theory of the monetary policy and neoFisherian stances.
The nice thing about macroeconomics is that no one is ever wrong.
29. May 2018 at 18:45
“In America, monetary policy in 2017 and 2018 became a bit more expansionary, despite higher rates.” This is so completely at odds with the narrative that one encounters *everywhere* these days that if you could get it widely accepted you would have to be considered the LeBron James of economic publicists. Good luck!
30. May 2018 at 06:15
Isn’t this a question of long run vs. short run, a film vs. a snapshot. If the economy has been contracting (or not growing at historical rates), then interest rates will fall because of expectations of future expansionary policies. Conversely, if the economy has been expanding, then interest rates will rise because of expectations of future contractionary policies. It also is consistent with the view that the market determines interest rates, that the Fed follows the market not leads the market. But this is very different from the claim that rising interest rates cause (or contribute to) expansion, while falling interest rates cause (or contribute to) contraction.
30. May 2018 at 08:29
Scott,
In case you didn’t read this two posts ago, I place it here. Is this a way to determine the natural rate and measure output gaps?
In large, diverse, healthy economies, the rate of interest on government debt should roughly equal NGDP growth expectations. Otherwise, the demand for and supply of money are necessarily in disequilibrium.
In monetary equilibrium, the opportunity cost of holding government debt is the nominal economic growth rate, given the zero-sum symmetry between rates of return on government debt versus the broad economy. Otherwise, the expected return on the value of the unit of currency versus output will be either too high or low, depending upon whether monetary policy is too tight or loose.
Does that make sense, or am I way off?
30. May 2018 at 08:50
Michael,
There’s no reason that the rate of interest on government debt should equal NGDP growth expectations. Even under the strong assumption of perfect foresight, the yield on government debt is the real interest rate in the economy times the gross inflation rate, while NGDP growth is RGDP growth times the inflation rate implied by the GDP deflator. There’s no reason that the real interest rate should be equal to the growth rate of real output, so your idea does not work. The problem is that the nominal return on capital in the “broader economy” does not have to be the NGDP growth rate in said economy, so your opportunity cost argument fails.
30. May 2018 at 08:55
Ege, Interesting comments. I should say that I am responding to the way that New Keynesians and NeoFisherians talk about policy. Thus New Keynesians talk as if lowering interest rates means a more expansionary policy stance, even if (as you point out) their models don’t imply that. I should have been more specific.
NeoFisherians also tend to reason from a price change, even though their model can be used in a way that avoids that fallacy. In previous posts I’ve pointed to one successful example of NeoFisherism, the Swiss policy change in January 2015. The Swiss know how to produce a low inflation low interest rate policy.
As far as the Friedman claim, he was talking about something entirely different. I think he understood that countries could stay at near-zero rates forever, given sufficiently deflationary monetary policies. Recall his optimal quantity of money paper. He was arguing that low interest rates created via monetary stimulus are not sustainable, and he was right.
In your version of NeoFisherism, which avoids reasoning from a price change, Friedman might have considered himself an adherent.
As far as interest parity, it holds well enough in the data (prior to 2008) for this exercise, which is looking at broad differences in policy.)
Rayward, You said:
“Isn’t this a question of long run vs. short run, a film vs. a snapshot. If the economy has been contracting (or not growing at historical rates), then interest rates will fall because of expectations of future expansionary policies.”
No, I think rates fall during recessions because of a sharp decline in the demand for credit. Rates fell during recessions even before the Fed existed.
Michael, The two are correlated, but not closely enough to be particularly useful in short run monetary analysis.
30. May 2018 at 09:27
Ege,
Let’s do a thought experiment. Let’s say the expected inflation rate is 0. If you had a choice between buying a 1 year T-Bill at a 2% discount, or a security that would pay you a rate of interest equal to a 3% expected RGDP growth rate over the next year, which would you choose to buy?
If the expected rate of return on the dollar versus GDP over the next year was -1%, because the previous trend inflation rate was 1%, then it’s a wash. Otherwise, why would anyone buy the T-Bill?
30. May 2018 at 09:56
Michael,
You’re confusing the RGDP growth rate with the real interest rate. These two are not identical. To see this, consider a simple endowment economy inhabited by consumers with identical preferences and with constant real output forever. In this setting, RGDP growth is always zero, and yet by changing the time preferences (for instance, the discounting factor in a dynamic program utility function) of the consumers you can make the equilibrium real interest rate be whatever you want it to be. The real interest rate depends on more than just the growth rate of output.
30. May 2018 at 10:12
Ege,
If I’m missing something, I apologize, but I don’t see what your idealized example has to do with actual economies. In an endowment economy with zero expected economic growth forever, there wouldn’t be a market for debt, would there? There wouldn’t be trading going on, presumably, because trading would create incentives for efficiency which could lead to growth. This would especially be true of an economy in which everyone had identical preferences.
Also, in real economies with heterogenous agents, there will be different temporal discounting for reward, with all agents having imperfect information and rationality, but in the aggregate that doesn’t have to matter. I think it was Becker who demonstrated in a paper in the 60s that even random agents can produce rational aggregate economic decisions.
30. May 2018 at 10:21
“In an endowment economy with zero expected economic growth forever, there wouldn’t be a market for debt, would there?”
There would be, because people would all try to borrow against the future to consume more today. The problem is that in aggregate they wouldn’t be able to, so they would only push the price of credit (the real interest rate) up without any net lending or borrowing going on. I’m giving an idealized example so you can see more clearly why your logic fails. The more complicated (and real world-like) you make preferences, the more reasons you get for why your argument does not work.
“Also, in real economies with heterogenous agents, there will be different temporal discounting for reward, with all agents having imperfect information and rationality”
Really? I thought that all real economies were inhabited by consumers having identical preferences and perfect foresight. How silly of me.
“I think it was Becker who demonstrated in a paper in the 60s that even random agents can produce rational aggregate economic decisions.”
That’s not what Becker proved. What Becker proved was that if agents sample randomly from their budget set, you get something which looks like a demand curve out of that. This is not a “rational aggregate economic decision”, and it only applies to this restricted example. I know some people have been doing more work on this, but insofar as this research program exists it seems to be about running log-linear regressions.
30. May 2018 at 10:33
Ege,
Just to be clear, in real economies, you’re suggesting the time preferences of individuals, for example, could make for risk-free real interest rates that are above or below RGDP, in monetary equilibrium.
So, who would loan money at less than he/she could earn from the average rate of return, on average? Who would borrow more than this rate, adjusted for risk?
If I’m just being dense, I apologize.
30. May 2018 at 10:34
And to be clear, I’m saying RGDP growth expectations, assuming no inflation, is the same as the average expected rate of return in an economy.
30. May 2018 at 10:44
“Just to be clear, in real economies, you’re suggesting the time preferences of individuals, for example, could make for risk-free real interest rates that are above or below RGDP, in monetary equilibrium.”
Yes.
“So, who would loan money at less than he/she could earn from the average rate of return, on average? Who would borrow more than this rate, adjusted for risk?”
This is a bit unclear, but I think you’re saying that if there are two risk-free assets out there giving different returns, people would not hold the lower return one. This is correct (well, mostly correct in the real world, but I’m willing to ignore arbitrage anomalies for now) and I don’t dispute this claim.
“And to be clear, I’m saying RGDP growth expectations, assuming no inflation, is the same as the average expected rate of return in an economy.”
This is the part of your argument that’s wrong. I’m using the perfect foresight case because if I don’t there are problems with the covariance of the consumption process with inflation and stuff like that, but even in the perfect foresight case this is still not true. It’s perfectly normal for a no growth, no investment economy to have a positive real interest rate if people prefer substituting consumption tomorrow for consumption today. In that case, if under my current consumption plan my consumption will be constant forever, and the real interest rate at which I can borrow is zero, I will borrow to consume more today and consume less tomorrow. When everyone does this, since reallocating consumption over time in an endowment economy with no investment is impossible, we get a very clean scenario in which all that happens is a rise in the equilibrium real interest rate until consumers are indifferent at the margin between borrowing and not borrowing.
30. May 2018 at 12:32
– Sheer nonsense.
– The FED follows the 3 month t-bill rate and that disqualifies the notion of “Expansionary intent”. The FED kept expanding its balance sheet (“Printing money”) since say the early 1960s. Yet, interest rates rose during the 1960s and 1970s and kept falling sine 1981. Where’s here the relationship ?
– Falling interest rates since 1981 would falsely suggest (according e.g. S. Sumner & M. Friedman) that the monetary policy of the FED was tight (even in and after the year 2008) IN SPITE of an ever expanding FED balance sheet.
– When I go through the exchange rate and interest charts then I fail to see a correlation (as mentioned in this post).
– I don’t take M. Friedman too seriously because he had some very strange ideas/fallacies.
30. May 2018 at 13:24
Ege,
Thanks for clarifying. I should’ve been smart enough to just take the general point you were making about the temporal dimension of consumption versus investment preferences.
Yes, I see no reason why an economy can’t have agents that, in the aggregate, simply have consumption versus savings preferences that mean the real risk-free interest rates are either above or below the real economic growth rate, even at monetary equilibrium.
And, I see no reason to believe such preferences would be stationary. After a long, deep recession, for example, preference for reduced consumption could increase for a prolonged period.
So, it appears the tautology I was asking about falls apart.
Thanks for the correction.
30. May 2018 at 19:20
Willy2, You are confusing levels with rates of change.
31. May 2018 at 03:14
OT but maybe not.
Okay, we have global capital markets and major central banks (Fed, BoJ, PBoC and ECB, maybe BoE and SNB). Heavy international capital flows.
MerrillLynch recently put out a report that global QE is now negative; that is as a group global central banks are shrinking their balance sheets.
Does a lot of macroeconomic thinking pre-date global capital markets, and, for example. the ECB?
31. May 2018 at 06:21
Scott,
Thanks for quickly addressing my question about the correlation between interest rates and NGDP, from an empirical perspective. I assume you’re referring to correlations like these:
https://fred.stlouisfed.org/graph/fredgraph.png?g=k257
You mention that, short-term, they’re not very useful for monetary policy, but what about long-term?
And what about the effective Fed Fund’s rate versus US productivity growth?
https://fred.stlouisfed.org/graph/?g=k0bZ
Is it silly to see a pattern in three recessions in which the Fed over-tightened, then under-stimulated, leading to extended periods of low productivity?
And look at Japanese productivity(expand to max range):
https://tradingeconomics.com/japan/productivity
Does that not appear cyclical?
So, in the case of the US, why don’t I have a good argument that monetary policy is still tight, due to the Fed’s expected reaction function?
31. May 2018 at 08:58
Michael, I don’t see interest rates as being useful in setting monetary policy.
Yes, productivity can be cyclical, but in the US productivity often rises during recessions.
31. May 2018 at 10:28
Scott,
Thanks for your quick take on that. Yes, productivity usually rises during recessions in the US, but then falls after the recessions end. My guess is that during the recessions, output lags employment by several months on the way down.
It seems to me though that productivity sometimes remains low for extended periods after recessions, like the Great Recession, and my guess is that structural factors are only part of the reason. I particularly think productivity should be much higher right now, even given shifts to service sector, the possibility we’re in a J-curve, etc.
But, letting inflation drift higher without a regime change, at least moving to a 3% inflation target, could be dangerous, given the Fed’s apparent habit of overreating to above target inflation.
13. April 2021 at 09:38
Interest is the price of loan funds (a free market clearing rate). The price of money is the reciprocal of the price level (the FED’s bailiwick).
Long term monetary flows, volume times transactions’ velocity, fell by 80 percent from Jan 2013 to Jan 2016. Oil Fell by 70 percent. DXY rose from 79.77 to 98.69, or by 24 percent.